Blogs
Our community blogs
-

- 13
entries - 698
comments - 78348
views
Recent Entries
Latest Entry
Reporting In The Blogs *updated*
Blog Reporting
In the past, before the upgrades and the downtime, reporting things in the blogs was a complicated mess of PMing BlogAlert, linking the content, describing the broken rules, and hoping someone read the BlogAlert account in a timely manner.
NO MORE!
The "REPORT" buttons on comments and entries DO WORK. Before the downtine, they did not. Now they do! Hurray!
So, in short, if you have something to report, click that button, describe the offense, and a blog staff member will receive the report and an automatic link the the offending content. (Please do not use this to report signatures)
This is much easier on us, on you, the general populace, and also on kittens everywhere.
-The Blog Staff
- Read more...
- 0 comments
- 13
-

- 6
entries - 9
comments - 71661
views
Recent Entries
 Latest Entry
Latest Entry
oh hey
look at that, there's no delete button for blog entries that you only uploaded to see if your blog still works
guess this one is staying up
oopsa doopsa
- 6
-

- 267
entries - 1695
comments - 156508
views
Recent Entries
 Latest Entry
Latest Entry
BZP T-Shirt Contest 2024
It's the 20th anniversary of the Metru Nui saga's beginning. So this years theme is the entire Metru Nui saga!
Toa Metru, Hordika, Vahki, Dark Hunters. Not just characters, locations, items, or even vehicles!
Rules: Your design must be a simple design, one color, and must be medium sized.
Your design must also be black on a clear white background. This makes it easier for the screen printing process.
You may post your entries in this thread, and have until the end of May to submit your design.
The Prize: The maker of the winning design will receive a free T-Shirt!
ADDITIONAL INFO:
The winning design will be chosen through a voting process of the members of BZP.
Colors will be suggested and chosen by the members as well.
Feel free to ask any questions if needed.
That's all for now. Have fun, and good luck!
- 267
-

- 19
entries - 15
comments - 1761
views
Recent Entries
- 19
-

- 6
entries - 23
comments - 7313
views
Recent Entries
 Latest Entry
Latest Entry
Embers - Project Teaser
I was recently reminded that blogs exist, so I figured that this was as good a place as any to post the first official teaser for an upcoming project that will be releasing later this year.
___________________
Deep down, everyone’s afraid of the dark.
It’s a powerful, primal thing, an instinct born long before any of us were created. In the dark, anything could be waiting.
A ravenous rahi, a roving Rahkshi, Karzahni or Irnakk or Tren Krom or any one of the other nightmares of legend.
But now we know there’s nothing waiting for us in the dark.
Nothing at all.
And somehow, that makes it even more frightening.
___________________
In this alternate reality take on the Bionicle story, the Great Spirit Robot was mysteriously shut down shortly after Teridax took over. In the wake of this second Great Cataclysm, lightstones and heatstones begin to dim and die throughout the universe, dooming its denizens to a dark, cold demise.
Metru Nui – with lifegiving light still seeping through the sun holes overhead, and its cold streets heated by the fires of the Great Furnace – becomes the last bastion for the Matoran species. But when the city’s Toa depart to rescue Matoran still trapped out in the dark of the dying universe, they leave the populace vulnerable to the machinations of an unexpected enemy, and return to a city they no longer recognise…
Work on Embers began in August of 2022. During that time, I was writing for my Farewell To Corpus Rahkshi collaboration, which put me in a nostalgic, inspired frame of mind, motivating me to finally act on some story concepts I’d been toying with for a long time.
Embers was originally envisioned as a trilogy of three “books” that I expected to be ready for release sometime in 2023, but the story ballooned massively in size and scope as I began work on it, expanding to six instalments instead. Due to my nasty habit of starting projects, getting overwhelmed, and not finishing them, I was determined to fully complete a first draft before I began posting anything. I felt that being able to go back and revise the story as a whole would also allow for a more cohesive and consistent narrative overall. As I post this teaser, I’m finishing off the first draft of Book 6. While I’ll still need to carry out a few editing passes (and probably completely rewrite some parts I rushed through), I’ll absolutely be in a position to begin posting chapters sometime later this year.
This is by the far the biggest project I’ve attempted and actually followed through on, and I’ve already got ideas for a possible sequel trilogy if the story is well-received. Keep an eye out on the Epics forum for the official release in the coming months.
- 6
-

- 1174
entries - 5958
comments - 128482
views
Recent Entries
 Latest Entry
Latest Entry
The almost-but-not-quite-annual roundup
And/or the usual "hey world! I'm still alive!" post

So where have I been?
Mostly busy with life, and finally with a stable internet connection at my PC so expect some more activity from me, I guess. Occasionally, anyway.Other than that, I missed this place, a lot. And can't help but get nostalgic about the old times of lots of daily activity. Regular display name changes, especially around April 1st (my, what a coincidence) or with whatever tiny trend floated by. (On a side note, I'm delighted to see that the old emoticons are still around. Love these
 )
)
Hope you're all doing well! I'll see you around. ^^
- 1174
-

- 8
entries - 12
comments - 1069
views
Recent Entries
 Latest Entry
Latest Entry
Cartoons and Escapism
Originally, this blog post was going to focus on Code Lyoko, but I have decided to expand it to be about escapism and fiction in general, since I have recently begun watching (and binging) Twelve Forever. There is a lot of behind-the-scenes drama regarding the show's creator that I won't be talking about. The show was first recommended to me by a former friend I no longer talk to back when it aired around 2019, but I have not sat down to watch it until now.
If you read my previous entry, in which I get all existential about BIONICLE and the passage of time, you won't be surprised to know that Twelve Forever resonates with me in a deep way. It captures in a visceral way how alluring and tempting remaining in childhood is. Personally, I think people have a bad habit of using "growing up" as a catch-all for a variety of unpleasant and frankly unnecessary aspects of modern life. It is nothing more than a thought-stopping technique meant to convince themselves that alienation from one's emotions is the norm and "adult." I never accepted it and never had any good reason to.
Twelve Forever and Code Lyoko both focus on a group of children (three, to be exact) who regularly travel to an extraordinary land. In Code Lyoko, this escape-world is the digital realm of Lyoko, where they must travel to fight X.A.N.A. and his monsters to save the world. Naturally, since it's a children's action/adventure show, it glosses over a lot of the unpleasant aspects of Lyoko that I'm sure are there--there is a broadly accepted theory that every time they "die" in Lyoko and get rematerialized back in the real world, all their injuries "catch up" with them and put them out of commission for a while. The purpose of the show is that, despite the fact that the kids are in life-of-death situations that kids shouldn't be in for real, the show's aesthetic and the way it is framed make fighting on Lyoko look awesome. In this respect, there is a significant gap between how the escape-world is perceived by the characters in the show and how it is meant to be perceived by us. BIONICLE and especially Pokémon are other examples of this type of storytelling. (In the case of BIONICLE, it depends: the Toa, for instance, are coded as adults as opposed to children. When we watch Tahu fighting the Rahkshi, the child viewer is meant to understand that this is more appropriate than, say, Hahli or Turaga Vakama fighting a Rahkshi. That does not mean that, at other points such as MNOG, the combat between Matoran/children and dangers is not similarly idealized as in CL.)
The Hunger Games is an example of a non-cartoon that does its best to subvert this kid-friendly combat aspect, to the point where it is something of a joke in the fandom that, if you glamorize and want to fight in the Games, you don't understand the point of the story. (Idealizing the violence is explicitly what the Capitol citizens, who while not evil are useless and naïve, do.)
Twelve Forever is not like Code Lyoko or BIONICLE. Endless Island is an escape-world for the main characters in the same way that the show itself is written to be an escape-world for the viewer. This offers its own unique comparisons to BIONICLE, however. Perhaps I was just a weird kid, but I always found the aspects of BIONICLE that were mundane to the characters in the story, like their homes and occupations, just as interesting as the major plot events and battles. I was so fascinated by the idea of lava farming, or the various mining disputes in Onu-Koro. MNOG in particular leaned into the everyday aspects of life on Mata Nui, the kind of things whose real-world equivalents children find painfully boring. SpongeBob SquarePants is another example of this method of storytelling: how much narrative finesse it took that show's writers to make working at the Krusty Krab, a greasy fast food joint, feel exciting for kids to learn about. As I grew up and did work service jobs, I was stunned to realize just how much actual real-world aspects made it into SpongeBob, and yet how relatable it still felt to watch. That, I suppose, is the ideal mark of good children's entertainment, something that does have meaning for adult viewers to recognize but, if it is unrecognized, does not make itself known.
The Fairly OddParents is on the other end of the SpongeBob spectrum. TFO is on a category of shows including Code Lyoko, Rick and Morty, or Regular Show, that are set in the "real" world until a catalyst, generally at the end of the first act, that signifies the "transition" to the fantastical. The difference here is that, at least in a show like TFO, the "point" is often that the fantastical has no meaning except in the ways that it mirrors the mundane. The show's formula involves Timmy having some problem, making a wish to try to fix it in an easy way, and the wish backfiring. The point of each episode is that Timmy either has to find a non-magical solution to his problems, or accept them as a fact of life. (At least at first, I haven't watched the show since Wishology.) In this way, Timmy Turner is the Zillennial's Sisyphus. In hindsight, what makes Cosmo and Wanda stand out most as characters is their status as Timmy godparents. They give him the emotional support that his actual parents are in most episodes too cartoony to meaningfully provide. The fact that they are magical beings feels almost like an afterthought, a non-personal role they just happen to fill.
Another show which Twelve Forever will remind the viewer heavily of is Adventure Time, the difference being that Twelve Forever explicitly contrasts the mundane and extraordinary. In the case of Adventure Time, which takes place begin to end in the extraordinary, the responsibility falls to the viewer to supply their own mundane reality as a contrast to the whimsical world of Ooo. That does allow Ooo to have its own BIONICLE-esque "mundane within the extraordinary." In a show like Adventure Time, that throws so much nonsense in the viewer's face, what remains in my memory the most are small details about Finn and Jake's everyday life, like how they have a non-electric icebox as opposed to a fridge, but ice is apparently valuable enough in Ooo that an established social convention is guests bringing their own ice. Another interest point which has lived rent-free in my head is the delicious food Jake is always cooking, like the everything burrito or bacon pancakes--weirdly normal human food in a world devoid of other meaningful references to modern real-world location and concepts.
There is a dark side to Forever Twelve. One thing which I have found vindicated in online reviews is just how weird, sometimes in a troubling way, Endless Island is. In the case of Adventure Time, since the weirdness is 24/7, it invites the viewer to "translate" the weirdness into a certain normality that Forever Twelve does not have, since Forever Twelve explicitly contrasts the weirdness with mundane reality. What Forever Twelve reminds me of most is Jack Stauber's OPAL. If you have not seen it, and enjoy psychologically unnerving horror, I strongly advise you to watch it. It's quite short and free on YouTube. All I will say is that, while the escape from reality into fantasy is normally whimsical and comforting in fiction, in the case of OPAL, it is horrifying. Forever Twelve takes place somewhere in the middle, with Reggie's dependence on Endless having a certain similarity to a drug addiction. The bland, colorless, and depressing way the real world is sometimes drawn in Forever Twelve only solidifies the concept. (See also: Coraline.)
This entry ended up being a bit longer and more rambling than I anticipated. Most of these thoughts are thoughts I have had in some capacity for years, which Forever Twelve only recently gave me the impetus to put to text. I increasingly feel that I myself use outlets like BZPower as my own Endless Island, or Time Before Time, escaping the constraining loneliness of artificial modernity.
- Read more...
- 0 comments
- 8
-
 Latest Entry
Latest Entry
19
-

I am not, and never will be ashamed of the cake puns in this blog entry title.
Anyways, it's been fun to look at milestones from the past 5-6 years of my baked goods journey. Please enjoy (vicariously) snapshots of gloopy sadness and glutenous glow-ups.My ego insists that I tell you about my natural dis-inclination toward exact measurements and the science-y part of baking (which is why I historically have had more success with cooking). But sharing sweet food with friends and family over the years has been a good motivator to improve, and there's nothing like a sporadic BZP blog post to share the progress

2018, for a sibling's birthday. This was back when I didn't know (or care) about pan sizes or icing consistency. My mindset was "It's sugar, flour, and more sugar. How bad can it be?" To be fair, it (probably) tasted good. I'm pretty sure we ate all of it, eventually. 😅

2019, for the same sibling's birthday. I had the vision, obviously not the execution. To be fair, it was a very hot summer that year, and I think this was my first attempt at homemade icing? But, yeah. ooof.
To be fair! It was eaten and did not go to waste!
2020, this sibling is very spoiled, and finally had a cake from big sister that stood up on its own!! Progress never tasted so good! (probably, I don't actually remember at this point what flavor this was)

2021, Valentine's brownie/cake. This is when I decided to care about form factor and presentation more. Boxed brownie mix and store-bought icing all around - two modern marvels that I will never cease to love.
2022! This is the year I stepped it up because suddenly there were in-laws to impress! Lemon raspberry cake, got my whole baking pan situation sorted and took homemade icing seriously. I've found the YouTube channels Binging with Babish and Preppy Kitchen to be the most helpful (educational, practical, and instructional), and you can probably tell!
But also, I found that I had more free time on the weekends with a job change. Moving from a physical warehouse job to a sedentary office job during this year was interesting - when I had a physical job, my hobbies outside of work were much more internal and sedentary. I got a lot of reading and writing done in these time period. When I changed to an office/teaching job, my hobbies almost immediately changed back to tactile and physical (knitting, cooking, baking, hiking). Funny how balance just kind of happens sometimes.
Pies, scones, muffins, cupcakes, and a few other desserts were also explored in this year. In a slightly broader scope, we also tried some fun international dishes at home, like pupusas, baozi, and spring rolls!

2023 cakes, and many other baking ventures happened this past year. Here are some of the highlights. It also helps that I changed jobs and had an office to share these baked goods with (as opposed to the old warehouse gig).
Apple Butter Maple cakes, from Preppy Kitchen. I actually broke a crock pot trying to make apple butter from scratch for the filling 😱
The small cake on the right is gluten and dairy free, and underneath the passable icing, was a DISASTER. Still learning the intricacies of the GF/DF world for the sister-in-law. Thankfully there are many box mix options now!!
Pink brownie cakes for niece's birthday. Had some fun with icing piping bags and nozzles, but have yet to actually get into decorating (may not actually happen. There's still that primal battle between "make it look nice" vs "it's all going to the same place", so there's a limit to my dithering.

Christmas Babkas! Technically not cakes, but after many attempts at sourdough that were meh at best, babka sounded like sufficient, sweet, and swirly compromise for a dough-based challenge.


2024 has yet to see large-scale baking productions - just some congratulatory oreo cupcakes to welcome a new nephew, and a batch of Hong Kong egg tarts that were a funky texture 😝.
Anyways, that's a slice of my life recently (wink!) and I'm always excited to hear suggestions, tips, or other tales!
-

- 2277
entries - 7675
comments - 472054
views
Recent Entries
 Latest Entry
Latest Entry
llllllllllllllllllllllllllllllllllllllllllllll
Any coffee aficionados here? Lately I've been drinking coffee in lieu of energy drinks, and I'm looking for different types to try. I'm not really into anything bitter, but I'm also trying not to use too much creamer or anything lol.
Also, sometimes my dog rolls onto his back while he's laying in his bed, and I got this hilarious picture

He just sat like that for about thirty seconds lol. He's whacked out
Can you believe tomorrow is March?? Goodbye winter avatars and banners... ;-;
- 2277
-

- 63
entries - 96
comments - 19124
views
Recent Entries
 Latest Entry
Latest Entry
Stuffed Animal Collection
I don't know how anyone would know this, but I adore and collect stuffed animals and have for as long as I can remember.
Might as well start with the OGs. Left-to-right: Gram Paul "Uncle Grandpa" Penguin, everyone's favorite old man who's gotten up in years and now needs a wheelchair. His son Fat Penguin (named long ago in a different time and place) who's probably the favorite animal I own. He's got a wife and five kids, but we don't need to talk about them right now. Glacier the walking ticking time bomb who likes to throw is little brother. Said little brother Iceberg who's a kleptomaniac and who only has one foot, but everyone swears he lost before his brother threw him. And finally their Italian cousin Gelato who's catchphrase is, "You guys are mean!" He gets to say it a lot around this lot.
A small sample of all my bears, the largest species in my collection. Rapid fire family left-to-right:
Germania Kirk: got his name from when me and my sister played "Star Trek", but afterwards we couldn't stop calling him Kirk. Is a preacher and married to...
Maple: The Canadian bear.
Dimples: their son who was the first bear baby in the world and is now a doctor. Everyone used to call him baby boy because he was the first.
Erin Erwin: the Irish ice cream man.
Millennium: Erin's wife and the undisputed best chef in the land.
Nikki: their daughter and now married to Dimples, hence...
Baby Boy: Dimples and Nikki's son who has his dad's old nickname. His catchphrase is "Ta da", which he is also sometimes called.
Not shown are the two Erwin family boys, Cuddly and Winnie. They moved away awhile ago and are living their best single life with their friend Curly.
Spangle and Brittany: I think I forgot their last name. Spangle used to be a superhero (Spangle Boy!), but now I think he just sits in his pajamas all day.
Caramel: their third kid and former cheerleader. Somehow fell in life with...
Sweeter: a gingerbread man and baker who can never match Millennium.
Lindy "Lucky Lindy": their daughter who's actually a clone of her mother because you know bears and cookies can't. Anyway, she's a bit of a trouble maker.
For whatever reason, most of my and my sisters' stuffed animal collections consisted of bears and penguin to the point that are few other animals were given the kind of offensive term "nonie" (NON-ee). Either way, the nonies' lot has improved over the years and Punxsutawney Phil has been the mayor for eight years or more. His chief advisor is his cousin Phil (the one without the hat) and together they wisely govern the town's treasury (the chests). The big monkey is their bodyguard Lazlo Khan and his little monkey son Bongo. The hedgehog is Lothario (that means "the lover") advisor/jester. The green thing is a recent gift from my sister that I don't know what to do with so I let him hang in the executive suite.
Also, Meltdown isn't there to hold the flag for them or anything he's just also on my desk and photobombed them.More recent additions now that I love referencing things. Left-to-right (back row), Pabu the red panda, Greywind the dire wolf, Bosco the black bear, Gojira the spinosaurus, and 51 the alien. (Front row) Bruce the shark, Lottie the axolotl and her son Verde.
I've just realized that my love for writing might have started with the stories and backgrounds I created around all these animals. Either way, this is a small sample of my collection, I probably have a hundred more, but what I really want to do is create some kind of archive of all of them with their names and histories to make sure I'll never forget. Will I find time? No idea, but this is a start I guess.
-JAG
- 63
-

- 55
entries - 112
comments - 72806
views
Recent Entries
 Latest Entry
Latest Entry
New Build: Winter Green
As the cold curses the land
She persists
For every winter that comes
There is a spring that follows
No chill has taken her
None will
For she is evergreen
More on Insta- Read more...
- 0 comments
- 55
-

- 24
entries - 124
comments - 18927
views
Recent Entries
 Latest Entry
Latest Entry
I did an art
Slinky through this linky on over to the comics forum to have a peak!
More to come maybe? Possibly? Who knows! The inner machinations of my mind are an engima. If I do continue it, I'm thinking of maybe having permanent guest stars positions, just for ol' times sake.
--Akaku: Master of Flight
- Read more...
- 0 comments
- 24
-

- 127
entries - 236
comments - 42817
views
Recent Entries
 Latest Entry
Latest Entry
???
I just got accepted into graduate school. My dream program. I feel excited, and I also feel guilty for feeling excited because I'm also still mourning. None of this makes sense.
- 127
-

- 36
entries - 68
comments - 18007
views
Recent Entries
 Latest Entry
Latest Entry
2023 Was an Amazing Year
Welp, time to reflect publicly on BZP. I always like doing that. This year, I'll be trying something a little different and I'll actually be typing this up while reading my private thoughts from my journal I wrote throughout the year.
Starting with something that was a theme throughout the whole year: In December of 2022, as part of a musical Secret Santa exchange, I received the song Where Are You Now by Danny L. Harle. From there, I listened to the rest of the Harlecore album, and then discovered the whole musical world revolving around the PC Music label/collective. I realized I already recognized a lot of the names from the 100 gecs remix album. This really is my kind of music. I found so many songs I loved, but one artist stood out from among the rest: GFOTY. She's quickly become one of my all time favorites and over the course of the year, I've listened to her entire discography. Unfortunately, PC Music announced that they're ending new releases on the label with the end of the year, so I'm listening to some of their stuff on the last day, even as I write this. It was a great ride, even if I only caught the tail end of it. Oh, and going back to the gecs, seeing them live was the other big musical moment for me this year. Their new album was great too.
As I mentioned in my last entry, I finished college, moved out on my own, and got a job. I feel a lot more independent now. With that, I've been doing a lot more cleaning and organizing this year for a variety of reasons. I've also had more time for my hobbies though, getting a lot more lego building done and integrating myself into a local lug.
I got dental implants put in at the beginning of the year. Something I had forgotten about was that this prevented me from eating my favorite food for a month. I'm actually just now getting scheduled to have the crowns put on the implants. I'm honestly tired of all this stuff going on with my teeth. I'm so ready to be done with it.
Something I'm noticing is I was able to become much more social and confident over the course of the year. I even went out on a few dates! Nothing that led anywhere serious, but I'm very proud myself for handling it in a way that felt very natural. Ironically, I'm also much more comfortable being alone now than when I was in college. I think there's something about being surrounded by people that actually makes you feel more lonely sometimes.
I've started playing more seriously in @Voltex's BZPGOT games this year. I've only recently started getting caught up on all the previous story there, but before I started that, I decided to read/reread all canon Bionicle story material. This, combined, with another event I'll mention later, means I did a lot more reading than has become normal for me this year. Next year I'm hoping to get caught up on the BZPGOT write ups, maybe read some other Bionicle fanfic ( @Pahrak Model ZX?) , but especially start reading some non-bionicle books aimed at adults haha.
Brickfair was great as I also mentioned in the last entry!
There was one thing about Brickfair I didn't mention though. At one point during the con, I got a call from my father. He met up with my cousin. I hadn't seen her in 7 years, and we hadn't been able to spend quality time with each other in even longer. He wouldn't tell me what was going on until I got back and spoke with him in person. It wasn't instantaneous for us to reconnect, but we did it. Both of us were worried the other might have somehow become a completely different person in the interim, but we get along so well. We were able to have phone calls, texts, and finally meet up in person for Thanksgiving. This has made me happier than anything else really, and I think it's been so good for both of us to have the other back in our life. I've always looked up to her, we have a lot of fond memories together, and now we're making new ones. She's someone I feel like I can talk to like no one else, and she always has such interesting things to say.
So that's obviously not everything, but that's the biggest stuff. Thank you to each of you who have had even some small part in making my year so good! And a happy new year to you all! I know I already have some good things planned for it.
- 36
-

- 426
entries - 1468
comments - 119238
views
Recent Entries
Latest Entry
20 Years Later...
Meant to stop by earlier this month for quick drop-in. I can't believe it's been 20 years since I first found this site. I rarely visit anymore, but I'm still alive and kickin', though I'm more active on other social sites.
The world has changed and so have I. Within the past decade, I got married and now have a kid.
So anyway, see you around. I may not visit much, but I haven't forgotten this place.
(C)1984-2023 Toaraga EAM
- 426
-

- 13
entries - 33
comments - 1497
views
Recent Entries
 Latest Entry
Latest Entry
more than meets the eye
So, i'm not sure what to put here anymore (spoilers: it won't be another movie review) but i may as well talk about some things
I'm Trans! (She/Her/Hers) It took me a few years to recognize it, but now i feel a lot happier than i used to- I feel like i'm the real me, for the first time in years.
I had been talking with my friends for a while and they helped me realize who i am, and i couldn't have done it without them.
i do intend to start HRT but the UK is pretty awful for this kind of thing lol, so i'm most likely gonna be waiting 5 years or so to just join the waiting list.
Until then, i've been thinking of posting some more things here, getting the use of my BZP account yknow? I have a lot of Mocs i've yet to share with you all (i dare say my skills have improved a bit since i last frequented these boards) and i look forward to interacting with you all once more!
-Bean
- 13
-

 Latest Entry
Latest Entry
October Oldish Occasions!
Okay, October Oldish Occasions! Wow! What an existence this beautiful spiral of life is. I guess this is a hello, life update and hopeful return to this lovely internet homey. Trying to see if easier for me to upload embed IG content instead of resizing. Which made me weirdly more okay with being more goofy on IG posting with main goal of it being for BZP blogging and likely only seen by around 3 humans, haha.
October art first, blobbyblogbog below it!
The doll obsession did indeed overtake my October!
WELL FAIL
on me figuring out embedding.
So Ugly links..
So sorry.
Does anyone know how?
to please help?
if it's possible?
did I already post this here, haha?
Candy corn caricatures of my mom and I from the glory of random craft trash, discount Go Grocery Avocado hot sauce bottles,their random black bags as a backdrop, and electric tape eyes. Salt lamp gift from family friends 🧡 The heights are accurate when I’m wheeling, haha.
@SPIRIT!!! May I tag to thank you overexcitedly with many virtual dance-a-happy? If not wanting to be involved in my weirdness I'll remove this! Thank you again for your genius! Every few-and-far-between human who enters the home sees it first thing and happiness it brings! EDIT:added the most important pic with their paper thank u sign sorry it’s shadowy/sunny bleached a bit hahaha



Apologies if unwated tagging here-can remove happily if any of ye request!
Shoutout to BZP bro @Bambifor remembering BZP birthday best wishes while I was barely alive! Thanks again! Coda (Anatolian Shepherd) 8x10” finished in September. 17.5hrs (mid medical episode art so snailstyle 😂). Pencil, mech’ pencil on watercolor paper. Thanks bunches to @otterfor allowing sharing (and for not minding lack of permission to pencil the pretty pet!).
So missed it here since a lifetime ago in September!
When somehow my everyday existence became a blur as I survived full blown falling into a rabbit hole without medical care (yet tons of prestigious doctors at Duke-who abandoned my case, ignored every near death plea for advice, said go to an ER-where the Mission hospital ER would discharge me, EDIT FEB 20 I just Google that place and found this hahaha (:https://wlos.com/news/local/mission-hospital-ncdhhs-report-details-patient-deaths-injuries-delays-care-asheville-health-centers-medicare-medicaid-immediate-jeopardy) still paralyzed and look at my limp body like I was lazy/wasting their resources and send a 7,000 bill that my cashier mom would try to pay ) and tried to retain consciousness in ER situations on a daily basis. Looking back at these months, it’s a miracle I’m alive. And my mom hasn’t absolutely lost her mind witnessing this. To be honest, I didn’t think I’d make it to 2024, I don’t think anyone did. I basically had accepted after the Jan 15 2023 stroke that I was unofficially on Hospice stuck on our couch and trying to make the best of it. In July I was tired of this, years of starving yet surviving due to my complex sickness. I decided to eat. Instead of controlling my symptoms by starving and waiting on Dulke diagnostic aid. I underestimated how severe the results of this would be, and am pretty amazed by the years of function prior achieved by miserable starving to control my diseases.
Not that getting in like 400-600 calories a day was much more than starving. Along with the daily 4hrs of fluid loss, writhing, hyperglycemia and that stranded me in a certain room that began to feel like a prison cell exactly 1hr after I dared bite into some delicious broth, vegetables, meat-or anything.
I was chugging two 2 liter bottles of electrolytes within an hour on the floor writhing…while my glucose was over 200 on no carbs while the fluid loss, LUQ pain, face flushing, etc raged. Every single day. An hour after eating, precisely-waiting to pounce on me. Clipboard art and crafts to cope while turning on The Frey Life videos on a shattered phone via YT. Wondering how other people live. Realizing how horrifying my own quality of life has been for years. Hoping to gain some insight on how human beings in a safe home life/environment on a daily basis live. What it even means to have a family support system.
There is a lot I don’t remember. There was a lot of lying on the floor, feeling possessed by some raging pain monster. Lots of being so weak I was barely managing to propel my wheelchair home alone. But not like anyone was there to help-my mom had to work or we’d both starve without having any social/family/medical support aid.
In like, September, on a week so weak I was wondering if it was my last, I rolled to the med drawer and grabbed my discontinued use Plaquenil for my UCTD, Undifferentiated connective tissue disease.
I started taking x4 the dose, 800mg. Have you ever been desperate to live? The daily GI fluid loss was cut to 2hrs daily instead of 4. My glucose wasn’t as bad. I told my good Duke rheumatologist and since then I've been prescribed 400 mg daily. The few pubmed articles I glanced at later support my positive experience with trying this- if I do have some form of endocrinology/cancer disease.
The horrors persisted, but more manageably. In October I got very excited and blasted Christmas music, decided to undertake doing a “real Christmas” this year in our new 101yr old family home! Because 2023 was the year of “home/life setup/seasonal decor totes/wow, normal moms have these things but mine never could”. So I started planning the holiday decor designs and working away on turning our old ornaments and junk in our Christmas trunk into things matching and new. I did a lot of ornament painting via the bathroom floor, (I have zero personal pride at admitting this, it kept me alive in such hours while unable to get ongoing medical care). .
My mom was trying to get me applied for Medicaid whilst the free-till won disability/SSI lawyer was still trying to prove I was incapable of surviving myself and needed SSI probably forever given Ehlers Danlos alone. My mom first applied me in mid 2022. My insurance ran out in January 2024 and my mom likely couldn’t afford to add me on hers at work. So we waited. I’ve been on Duke full financial aid for years, but also parent insurance deductible payment stuff and ER bills on them/now just Mom.
Mom-She finally got legally divorced in October ‘23, so grateful. What a wreck. Exdad still won’t sign over the retirement bit, or her mom’s inheritance car to her so it’s a nice lawn ornament, haha. The car on which he canceled the insurance on in late July-stopping us from driving legally, forcing her to buy a new old car, stopping my mom from renewing its insurance it not having the title of it, & stopping getting med help for me for the new daily ER fluid loss emergency. He didn’t know this stranded me into a life threatening crisis. He didn’t/doesn’t know this. I shudder at the scales of justice, so thankful to have survived it. So strange to me that someone like him would be sent a disabled child-He so often cruelly said to people “Did your parents have any kids who survived to adulthood? Bet they regret that!”...I have somehow, thankfully been one such personage surviving so far to this age, in spite of every arrow aimed at me. And found out in such situations there are endless ways to be personally happy-It’s an inside job! . I’m not even surprised any of this was done. Weird how you can see so much sadness it becomes easy not to even react.Anyway, sorry, hope it doesn’t sound angry- I’m not, just the unfortunate events in a chronologically current recording.
Takin' a drive, I was an ideal
Looked so alive, turns out I'm not real
Just something you paid for
What was I made for?
Some day those legal papers will come, perhaps, but tisn’t exactly pressing. Each time anything moved on the legal stuff it was a backwards breakdown stress spiral for my mom. I am grateful to say these horrors are now over, and things are much better! Now we can happily go on living, as if certain people in life don’t exist, without being every sec’ reminded of it, each conversation being about it, and go on enjoying that things are at last settled, safe and right. (EDIT: MID FEB ‘24: Car paperwork at last acquired, mom sold the sabotaged lawn ornament at last! Insurmountable gratitude!)
Medically, nothing was changing except one day I got super hungry, ate a lot of walnuts instead of the just like 500 cal daily meal that nearly killed me. My throat closed and the extra bad face flushing again. The Epi-triggered and resistant “anaphylaxis” again. The whole suspect Carcinoid Crisis again. Since 2020 that ugly thing. ER at Mission hospital, 6 am. Oct 16th. I made medical info cards a week prior because I’m tired of trying to explain my diagnoses. This thing is effective (RIP privacy when sickness shreds the remaining “dignity”. I now have 3 laminated and take to appts. the dysautonomia diagnosis new since September tilt table test. ). . I told my mom to ask for Octreotide. My mom mistakenly thought my allergist had suggested this, told them so . He did not. This was my own research. I could barely breathe much less tell them this. They gave octreotide and my airways opened up. I went home. Allergist appt to rerun allergen labs to be sure, like 1 lab order from my annoyed primary care doctor for the fluid loss. Still not allergy or high Tryptase.

So my good allergist (guy who found my tick bite Alpha Gal allergy saving my life so long ago), was like “yeah, still looks like carcinoid/a net tumor, especially given this, smart move on the Octreotide!” haha. So I contacted him later and my good rheumatologist for Duke and UNC GI cancer and new repeat endocrinology referrals for carcinoid/NET tumor/Possible diabetic condition. And UNC approved my mom’s full financial aid application for me! So since I’ve waiting on those to get scheduled some day, a new GI doctor appt at Duke in April (I had to fire the one Duke GI lady who left me to pretty much die after years of telling me it was surely Celiac disease and “just one more EGD, enteroscopy, etc”.)
I still had a useless Duke primary care dr 3hrs away, but we were unsure who to use here given the digital Mychart records needing to be accessible and making sure Medicaid would cover if I was approved. So I waited.
My high glucose raged during all this, I’d eat carrots or peas and it would go over 180. Tiny amounts of carbs sending me over 220 and half conscious symptomatically. I tried so many different foods, tried breaking it into two tiny meals to see if the GI got less angry, but nothing. So broth, protein, vegetables, and stevia seasoning became the mainstays while the glucose, face flushing, hyper thirsty, and GI episodes continued to rage on starving level calories. (Like 600 calories daily, robbed of yummy things). Meanwhile my frightening since-September 80-82lb weight just maintained. I’m 5’4”. Prisoner of war aesthetic going on there. Oh well. Alive!
Thanksgiving!a brief bit about it, i’ll blog content beyond October later, just a general update trying to grasp the spiral of this! I’d barely finished most of the decorations for the day , got to wear the vintage granny clothes I adore from my new 80+ yr old mom’s aunt (weirdness of mom being adopted) and it was wonderful with my mom off-day. We watched livestreams from ActionKid of the Macy’s Parade while eating POPCORN in our new popper & putting up the new upcycled decor by me (later to be blogged). We had such good times. One of the best thanksgivings I remember. Actively FB messenger spamming my brother. Every holiday prior was just the 4 of us and major medically-dietarily restricted/we just didn’t do anything. Also, prior, my ex dad hated the traditions, seeing his family at holidays, birthdays etc. and my mom had none aside from her peculiar puppy mill owner estranged mother and prison brother.
So getting to celebrate “real family holidays” in a gloriously nontoxic home environment is not something we’ve really experienced (except for my mom, as a child) before. It was a dream. I finally don’t feel unsafe 24/7! Near heaven! The 2022 thanksgiving prior I tried to pull out our old Xmas decorations but just cried instead over the shambles of our lives. 2023 thanksgiving was a DREAM. We are actually very much recovering and learning to live. If we’re all still around next year, I think it may be ever better!
I decided to make a traditional thanksgiving dinner, immediately freezing some dishes for Christmas. Decided to eat tons of whatever and everything I wanted that day, even if I went into a coma. That went SO badly hahaha. I took extra plaquenil. No regrets. Totally threw up. Eating is torture but so worth it.Would do again. I felt so alive, it’s so nice to eat with other people. I had no idea how poor not being able to eat together makes the “quality of life”. Wrote a disturbing song in the stupor that followed that I’ll later repost, hahaha.
And then after that Twas all out Xmas mode-still…Making some rushed decor, decorating the new old hold for the first time, trying to color theme each room!, lots and lots of cooking and baking! Pinterest recipe bliss! Planning excitedly for my brother to visit after not being able to for a year. The first time the home wasn’t even fully renovated and we didn’t do much of anything, decor or food wise. This meant unplanned renovations and rearranging of the kitchen to be more disabled/wheelchair friendly to reduce my suffering,haha.
The “Cook Nook” was evolving- my cozy cottage closet wheelchair workspace! Such kitchen shuffling. Still a work in progress. (EDIT FEB ‘24..Done!)My mom getting me an instant pot has massively helped me given my inability historically and now especially to stand long at the stovetop. Need to take updated pics and add to this. Also, I am relearning how to cook via food scale using mostly metric, for ease, fewer dishes, and nutrition calculations. Thanks to King Arthur Flour recipes for encouraging this. I am relearning how to calculate the servings/nutrition on my own recipes and all recipes once again (one day I won’t have to Google nutrition on 3oz raw “x” every time). I did this from 2017-2020 (post severe food allergies + ingredient label checking drama, PICU, hospital) as per my illness and appetite never existed, and I was scared I’d accidentally lose weight and almost die again. Then in 2020 I just became major sicker, unable to eat enough for a normal creature to live, started gaining weight, then the celiac train wreck began. So all this nutrition content stuff is major Deja Vu.
Sometime in December? We found out I got approved for Medicaid , and now it appears to be because the US government has officially accepted that I am disabled/useless in working society. I am so grateful and honestly cannot believe it. It seems like I may not have to show up in virtual SSI court in March now for the disability lawyer to “prove I’m disabled” from showing my medical records that the government already has. (EDIT FEB ‘24: Virtual court date is a day after my b-day, perhaps I can control symptoms enough to eat cheesecake & take sickness a day prior if I completely dehydrate, haha? Yolo or no? )
So in December the try for local primary ensued. My mom is doing all the paper and scheduling work as usual (cannot Adult). I went to one nice doctor on December 7, broke down crying weirdly over my situation (normally numb to the chronic near death experiences). She was amazing, but couldn’t accept me-I needed an internal Med-Ped doctor to “accept my case” as I was “too medically complex”. Mom’s Hunt ensued, I got an appt. in the UNC based local system that linked with mychart & their better ER 30 mins away.
I went to their ER for labs/my chronic emergency level fluid loss and malnutrition on Dec 13, like: “hi I have no primary care yet please help.”
That was useful, hadn’t had labs since September. They’re all rough as one would expect, but I’m managing to keep my electrolytes acceptable with salt cravings, bullion and lemon water.
Basically: The internal primary care appt. Finally came! It was, to my horror- a male doctor. I vowed to never have another given a few terrible experiences with them due to my age, gender and being underweight (as if I chose this nightmare-then I blame myself for it, though it’s not something I can control/fix.). which had been up a full day prior so was very out of it. The ER labs were useful for them, too. The intern doctor had an intern too, who was very nice and shockingly interested in my load of recent medical notes and since July daily recording diary of my food fluid, med and intake and vitals timebook. The book I made out of desperation trying to figure this out or find someone who could. Shockingly, they gave good advice and accepted my case! They understood Ehlers-Danlos, amazingly. They asked what I wanted to start on, I begged for help on eating and drinking. He said the human body can process ~20g protein per two hours for muscle building/retaining, and with my weight & intake tolerance being so low I definitely had muscle wasting (I, who only ate 4 slices broth and bread daily-for over two years while desperately waiting on Duke GI doctors to figure out this wasn’t celiac and why food made me so sick). Apparently ill & old people die from bowel necrosis due to muscle wasting in situations like mine. No other doctor ever mentioned lacking protein or muscle wasting making everything worse. Duke doctors gave no aid aside from “I can send you to a dietician if you’d like it”-as if generic advice would aid the unmanageable food reactions. Also, male Dr was awesome not a nightmare. AWESOME. He saw my real actual email which literally contains Sarasbabyducks given my past pets, and he saw that& was like EPIC I RAISED RUNNERS, what breed did you have? Beautiful carcincle Muscovy, Ancona and Pekin were so loved by wee me. Given struggling to verbally communicate my mom also 2nd visit was like “we think she’s autistic- and my doctor IS FORMALLY DIAGNOSED and told me this!? I also found his IG sand apparently is into alternate herbal things & didn’t roast us for desparate experimenting!
The new doctors don’t know why my glucose is crazy high, and said I was allowed to try carbs with the high protein and see what happens/monitor it.They also bumped the UNC endocrinologist referral up for Carcinoid/NET tumor/possible atypical diabetes and scheduled a six week later progress check-this is unheard of in my life to have ongoing medical follow up, help, or doctors who genuinely care if I live or die. I am so grateful.
I also got clearance on my plan to eat YUMMY HOLIDAY FOODs during Christmas week when my bro came and not monitor vitals/anything! So prior to bro visit, I embarked (cautiously so Christmas plans wouldn’t be ruined by me being sicker) eating at least 20g x3 daily and increasing my foods/trying some fruits/vegetables I normally get hyperglycemic from. Shockingly my glucose and GI episodes improved some. It’s so hard initially to learn how much protein’s in what. Then Christmas! The so longed for first real family Christmas in the new old home, fully renovated! Bro came a day later than hoped (traffic), but made it on Xmas eve night! I’ll later blog of it! On Xmas week I tried to eat all the yummy foods unrecorded, mostly! It was a delicious disaster haha. Been Still recording glucose x3 daily, but thankfully not fluids or blood pressure now. That was tons of exhausting work, especially when barely functioning already. Getting back to the protein!...
This concludes the illness fog written content mostly from goodness knows when! Free to frolic on to editing the somewhat later project photos as a hopeful attempt to reawaken my brain from months of hours-daily medical meltdown endurance without local care access. Grateful to be in this beautiful world, for my mom, Medicaid approval, new Internal Med doctors, and the few pretend friends who perhaps, for some reason, are kind enough to read the ramblings of a happy hermit, sick lunatic.
This is where I stopped writing, haha.
Current tiny update February ‘24, I’ll fill in gaps later if I get the chance!: Jan. 2 I started some alternative herbs and medications my mom had been considering, given doctors not helping and time running out .Things supported by scientific papers and research, a hopeful cure if carcinoid tumor/pancreatic cancer. 3 herbal pills and 2 fluid meds. My glucose at least is starting to markedly stabilize (FEB update)! Supposing it’s the combined CBD, my DIY-not-to-die plaquenil, tumeric and berberine along with the other high powered liquid thing? The hours of horror fluid loss GI wise are harder to survive as I’m trying to eat more-some days I got in 1000 calories-a miracle for me. I was in the new awesome UNC ER again Jan 13? after eating in a restaurant for the first time in 6 years-a glorious event for me to leave the home at all! For a funeral of my honorary granny. Backed up to my ribs despite chronic fluid loss-surprising and why it’s like glass shards in ribs when eating or drinking often. I’ve been out of it since and barely able to eat given my GI being badly broken, now require a new old people med device to somewhat more safely stay home alone, but now, mid Feb, feel like I’m coming out of the fog. No regrets, the restaurant was delicious! And now I’ve local GI care from UNC helping & as I write this current bit I’m leaving for my first combined colonoscopy & EGD done simultaneously later today. 6? EDG & enteroscopies and one colonoscopy at Duke from 2021-23. Issues found but no helping. Hoping they aren’t scared to fully sedate me here, haha. That only other 2022 Duke colonoscopy..Then the guy just blamed me for being too skinny, and was unable to find anything structurally, not being able to complete the procedure fully. I was half conscious and in pain screaming, when supposed to be all out anesthesia’d. Extra fentanyl this fine day of February, please! Also weirdly, my parent's equitabled distribution disaster was precisely 1 year ago today-When DVPO exdad dumped all my old & future medical bills on my former homeschool medical mom & attempted to take everything, almost suceeding after we were forced to flee homeless in 2022 to survive him. No support financially, what is mythical alimony and good lawyers? My mom having horrible mental breakdowns. Why exdad. I almost wheeled then walked out into traffic after this, no one in my life has ever made me feel more worthless and like a burden for breathing the air. How can one cope with being a burden to their own mother? This was post Jan 2023 no-med care post stroke when I could barely move, drink, swallow, eat or talk. Home alone surviving on the couch with a pencil in my hand giving me the will to try to “live to give, live to love” in little ways-if nothing more on earth I could say for.
Turns out I'm not real
Just something you paid for
What was I made for?
But somehow, we stuck together and smiled after the storm. So grateful she got her mother's ex-puppymill and land, a little lumpsum, and we have blessed freedom!
Anyway, tis all my bitty remaining brain cell can summon at the moment! Life is honestly improving so rapidly this year it’s dizzying! Being able to even blog a bit (even if a bit off-balance) is proof of this! local good drs, hope to survive/cure the one thing, getting to often enjoy family meals with my mom-never allowed historically ( medical and family toxicity situations), finally finishing the few leftover home renovations, the first year she’s fully divorced finally and mostly financially in an area of safety! I’ve dubbed it the year of (my mom’s) Julie’s Jubilee with laughable glee! And I’ve given the home and acres around it a loving dub of “Misfit Meadows” I am indeed making a sign for our front room, haha! So weird to be allowed to be in a home so happy!
I absolutely apologize/will edit if it’s not allowed to be so real here, or if this content isn’t BZP friendly. And for photo embed fail pleasehelp? I have no perspective on what it's like to live as an ordinary person or how rules apply here. ‘Appy impaired unaware alien here. Virtual hugs to all, tis all! Missed blogging in the BZP beauty where I can be a misfit with so few openly judging me for the fairytale ramblings, thanks to all thee!
"Think I forgot how to be happy...
..something I can be!"
- Read more...
- 0 comments
-

 Latest Entry
Latest Entry
Masks of Power
Checking out the new Masks of Power trailer made me really nostalgic for my old BZP days. I really miss the huge community we used to have. I always say I'd like to come back into the fold, but I haven't committed yet. Bionicle has always had a special place in my heart though. Not to be dramatic but I feel like it really shaped part of who I am. After everything that's happened to me, through life and work and new relationships and long gone relationships and the discovery of my true identity, I am still a Toa warrior 💙💗🤍💗💙
-

- 1066
entries - 5317
comments - 730059
views
Recent Entries
 Latest Entry
Latest Entry
Bionicle Day
Today is #810nicleday and so I thought I might use this opportunity to visit this old place to once again share some of the artwork that some fantastic folks have done for the campaigns I run over in the BZPGOT Discord server!
But first things first: an invitation. If you're interested in potentially participating in any future games (or simply want to hang out with other Bionicle fans), you can click the invite link to join us!
Anyway, onto the art. Today I wanted to highlight the series of covers that I commissioned for Verdant Wind two years ago. If I've done it right, you should be able to click the image to see a higher resolution.
Verdant Wind was the ultimate culmination of five years' worth of stories. It served as a grand finale for every character and story that had appeared up to that point, and to celebrate the occasion, I commissioned several covers for it.
The first cover, done by @TBK, is the official cover of Verdant Wind. It features the leaders of three player factions standing off against the game's main antagonist, with the broken pieces of my own NPC's mask in the dirt behind them.
The first variant cover, done by @ToaTImeLord, features those same player characters standing off against each other - fitting, as Verdant Wind brought them back into conflict before bringing them together.
The second variant cover was done by @xccj. In addition to the leaders, this cover features much of the other player characters - those who made up the core cast of the Edge of Dawn arc.
The third and fifth variant covers were done by some of my IRL friends (and yes, that fifth one is watercolor!). Both feature the faction leaders.
The fourth variant cover was done by @ZippyWharrgarbl. Like Xccj's cover, this one features much of the player cast, with a couple cameos and secrets sneakily inserted as well.
The sixth variant cover was done by @Jakura Nuva. It features the three player faction leaders being crushed beneath the game's main antagonist.
The seventh variant cover is a unique one; I commissioned it later than the others, as Verdant Wind reached its halfway point (and the big twist that would come with it - one that ultimately united the entire game world together). @Akaku: Master of Flight did a fantastic job bringing it to life; it features a set of characters who together represent every era of the games up to that point, working together.
The eight variant cover is also unique. I am responsible for the design, but I take no credit for the artwork used - that's all TBK and Akaku.
Anyway, that's all for today, folks. Hope you enjoyed!
- 1066
-

- 353
entries - 2639
comments - 159318
views
Recent Entries
 Latest Entry
Latest Entry
Strange Bionicle Find
Recently I managed to find someone selling the Bionicle Quest for Makuta board game online. It was in pretty good condition. An excellent addition to my collection.
I also picked up a few other board games. Just something to do with the kids I work with. One of the games was Monopoly. What did I find inside the box?
A single Cordak bullet.
The evidence speaks for itself. Family game night turned violent, the Toa Mahri intervened, and there were no survivors. 😔
Open and shut case.
Bake him away, toys.
- 353
-

- 812
entries - 3372
comments - 356098
views
Recent Entries
 Latest Entry
Latest Entry
I'm Building Lego on Twitch!
Hey, all! I'm still alive and kicking! I hope you are all doing well as I know it's been a long time since my last visit.
Life has been uh... or I guess continued to be crazy? But things are mostly pretty good right now, there is still a lot that could be better but I'm still here and trying to move forward. My last entry was 2019... so a lot has happened. I'm back in my house thankfully. It's not perfect but it's livable so that's a good thing. Housing was questionable for awhile from hotel to RV to another rental. I'm a manager at a pharmacy so that's unexpected and I guess interesting. On April 4, 2021 my father passed away so that's been tough especially as we just passed the two year anniversary of that so Tuesday was a hard day. But I met more new friends and people I care about and twoish weeks ago we hung out for the first time and that was some fun that I found was sorely needed as I haven't done something like that in a long time.
There have been ups and downs as that's life.
Lately though I've been streaming on Twitch! I've recently become a Twitch Affiliate and early in the year streamed some Lego Building.
And on Saturday I am going to be building a few sets on stream at 1pm ET!
We're building:
40581 BIONICLE Tahu and Taku
40516 Everyone is Awesome
... And a couple more but one of them is unofficial... but for Bionicle fans of 2004 should be very familiar.There is a whole tweet that announces it and hints at it right here.
I also plan to giveaway a few small sets I have during the stream. (It's nothing too huge but it's still free Lego.)
I also stream video games with a lot of friends. So if you like that kind of thing feel free to check it out.
If you feel like joining the Lego stream will be at 1pm over on my Twitch channel!
And I'll try not to be a stranger.
- Read more...
- 0 comments
- 812
-

- 190
entries - 495
comments - 72883
views
Recent Entries
 Latest Entry
Latest Entry
An adorable new acquisition
I've been wanting to get a copy of the original WALL-E set for a while now. This morning a local independent Lego store got one in and I couldn't resist!
The box is in absolutely mint condition, like it just came off the shelf - and it's staying that way! Won't be building him anytime soon, if ever. He was a bit pricey, but I traded in a few sealed sets that I had duplicates of to make the purchase more palatable.
Now I need to get the new Brickheadz version!
- 190
-

 Latest Entry
Latest Entry
Hello
Dropping in again for no reason, seeing who's about. Still a few folk I remember doing similar now and again, kind of nice.
Been doing some self-reflecting recently, bit of therapy and that, you know how it is. Probably should've been doing that as a teenager but eh, better late than never. Actually brought up this place during a few sessions, was very much a place I turned to to be 'validated' when I wasn't getting that elsewhere in my life. Growing up I had nobody around who shared my interests and a lot of folk who just thought I was dumb - so BZP gave me a place to have shared interests, and be seen as 'smart' for knowing a lot of Bionicle lore. And then the 'popularity' and 'fame' I'd get leaking set pictures or kicking off for gay rights or whatever was giving me the attention I wasn't getting elsewhere. And there'd be a bit of a 'fight' mentality in all of that because of dissatisfaction elsewhere in life. A lot of the motivations and brain loops involved back then have persisted over the years - getting quieter, but when I step back and look I can still see that stuff is cycling around in my head a lot. People's opinion of me informs a lot, I do a lot to be valued by people and react badly when I even get the WHIFF that people think I might be dumb or not understand something - it's like I have to 'prove' myself in those situations. It's all able to be traced back, and seeing this stuff laid out like that and mapping it all back just makes it all a lot easier. I can see how my brain naturally functions, and why.
Wiped this blog because I mentioned it to a few people IRL and they tracked it down, them seeing how I used to be was not a comfortable thing so I panic deleted as they started reading. Bad times. It's tricky with new people, you get the fresh start with them, but having a previous version of yourself 'preserved' online for them to also see is....yeah it's weird innit.
Anyway, things are good overall. It's cool analyzing myself a bit more - always growth to be had, just trying to actively dig for it a little bit more at the minute. Pretty fun and cool.
Also, you know what I'm desperate for? A run-down of like, what happened with every BIG NAME person from BZP back in the day. I wanna know where everyone is and when they dropped off the site and why etc. I live for the GOSSIP.
-

- 610
entries - 1306
comments - 416481
views
Recent Entries
 Latest Entry
Latest Entry
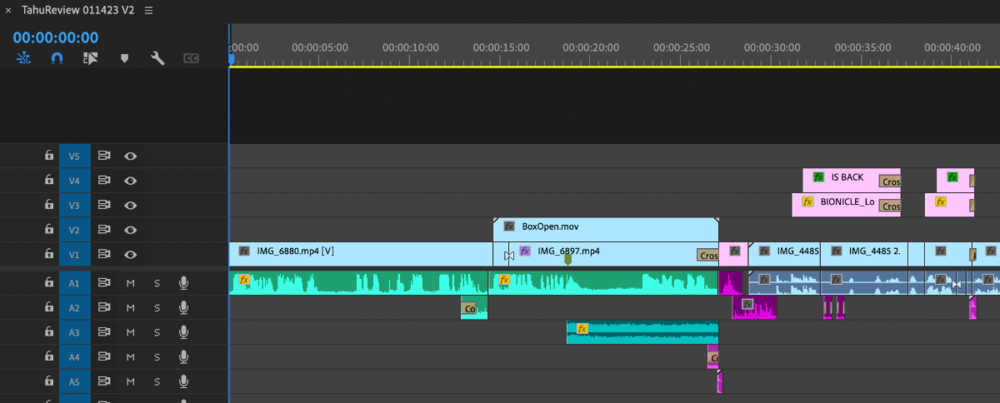
A Professional
Well, after a brief Invision Board-based hiatus, we're back!
Did you like that video review of Tahu and Takua? I haven't done one in a while and it was fun to dive back in, especially since, over the past year, I've moved to doing video post-production full time. I was freelancing for around a year at a couple of documentary houses until last month when I started as a staff Assistant Editor a trailer house. If you saw the trailer for Indiana Jones and The Dial of Destiny, that was us. I had nothing to do with that Indy trailer, but I did see a TV Spot I helped out with on TV on New Year's Eve, so that was pretty dope. There are a lot of projects in the pipe that I can't talk about (I'm NDA'd within an inch of my life) but it's super cool to, y'know, be doing this professionally.
Part of the fun of the gig is getting to see how those trailers are made and see all the ways the Editors make them work. And then learn from them and use them when cutting something else.
Like a video review for a Bionicle site.
I put more effort into this than the other reviews I did, part because it's Bionicle and part because, well, I wanted to take stuff I've learnt out on a semi-dry run. There was an AfterEffects project too to enhance the glow in the opening too, plus some foley and externally-recorded sound. Then some funky sound design too 'cuz this stuff is fun.
Because hey, I am a proper professional.
- 610